Modelowanie matematyczne
- daje szybką odpowiedź na postawione pytanie (w rzeczywistej sytuacji decyzja trwa lata);
- zapewnia możliwość szeroko zakrojonych eksperymentów (wdrożenie w prawdziwym obiekcie jest często niemożliwe).
Zasady udanego modelowania matematycznego:
- Weź pod uwagę główne właściwości symulowanego obiektu.
- Zaniedbuj jego drobne właściwości.
- Aby móc oddzielić główne właściwości od drugorzędnych.
Przykład modelu matematycznego
Zadanie. Zaprojektuj zbiornik o kształcie prostokątnego równoległościanu o objętości V = 2000 m3, tak aby można było wykorzystać jak najmniej materiału.
Decyzja .
Objętość zbiornika można obliczyć według wzoru: V = abh, (7,1)
obszar S = 2ab + 2ah + 2bh (7.2), gdzie a, b, h są bokami zbiornika.
Takie oświadczenie można napisać: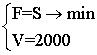 
(7.3),
co czytać: zminimalizować wartość S, pod warunkiem, że V = 2000. Zastępując w (7.3) wartości V (7.1) i S (7.2), uzyskujemy: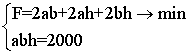 
(7.4),
Dodajemy oczywiste, że a, b, h> 0, otrzymujemy model matematyczny: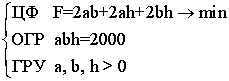 
(7.5)
gdzie: TF jest funkcją celu, OGR jest ograniczeniem, GRU jest warunkami brzegowymi
Ogólny przypadek problemu optymalizacji
Oznacz x1 = a, x2 = b, x3 = h, a następnie piszemy: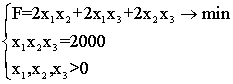 
(7.6),
Oczywiście (7.6) można napisać: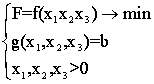 
(7.7),
Następnie możesz to napisać ogólnie: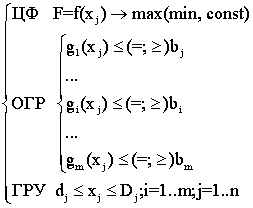 
(7.8),
System (7.8) można zapisać bardziej zwięźle:
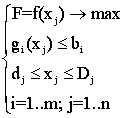(7,9)
Rekord (7.9) to ogólna forma pisania zadań optymalizacyjnych. Ten system obejmuje trzy komponenty:
- FC jest funkcją celu lub kryterium optymalizacji, pokazuje, w jakim sensie rozwiązanie powinno być optymalne, tj. najlepszy Jednocześnie istnieją 3 typy przypisania funkcji celu:
- Maksymalizuj
- Minimalizacja.
- Przypisanie danej wartości.
- OGR - ograniczenie, ustal zależności między zmiennymi. Mogą być jednostronne: gi (xj) ≤bi lub dwustronne: ai≤gi (xj) ≤bi. Ponadto każde ograniczenie dwustronne można zapisać jako dwa jednostronne: gi (xj) ≥ai, gi (xj) ≤bi.
- Gru - warunki brzegowe. Pokazują granice wartości pożądanych zmiennych w optymalnym rozwiązaniu.
Rozwiązania problemu, które spełniają wszystkie ograniczenia i warunki brzegowe, nazywane są dopuszczalnymi. Jeśli model matematyczny jest poprawny, będziemy mieli kilka dopuszczalnych rozwiązań.
Ważną cechą problemu optymalizacyjnego jest jego wymiar, określony przez liczbę zmiennych n i liczbę ograniczeń m. Stosunek tych ilości ma decydujące znaczenie dla sformułowania problemu optymalizacji. Istnieją trzy możliwe relacje: n <m, n = m, n> m.
- n <m
na przykład: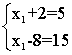
Tutaj n = 1, m = 2. Jest oczywiste, że takie problemy nie mają rozwiązania, z wyjątkiem przypadku liniowo zależnego układu równań: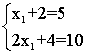
(tak samo jak w przypadku 2, gdzie n = m = 1) - n = m
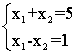
Tutaj n = m = 2. Istnieje wyjątkowe rozwiązanie, z wyjątkiem przypadku liniowo zależnego układu równań: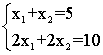
(tak samo jak w przypadku 3, gdzie n = 2, m = 1) - n> m
x1 + x2 = 5
Tutaj n = 2, m = 1. Istnieje nieskończona liczba rozwiązań.
Ponieważ większość ograniczeń jest zapisana w postaci nierówności, rozważamy na przykład następującą nierówność: x1≤5. Wprowadzamy dodatkową zmienną y1≥0 i przechodzimy od podanej nierówności do równania: x1 + y1 = 5 Dla tego równania, n = 2, m = 1, a zatem ma nieskończoną liczbę rozwiązań.
W ogólnym przypadku GER ma postać: gi (xj) ≤bi i = 1..m; j = 1..n;
wtedy mogą być zapisane w formie: gi (xj) + yi = bi yi≥0; i = 1..m; j = 1..n.
W tym przypadku całkowita liczba zmiennych xj i yi równa N będzie wynosić: N = n + m, a liczba równań pozostanie taka sama jak m.
Oczywiście, N = n + m> m, a system ma niezliczone rozwiązania. Jeśli więc ograniczenia są nierównościami, system zawsze ma nieskończoną liczbę rozwiązań.
Tak warunek n> m jest niezbędnym wymogiem problemów optymalizacyjnych.
Optymalne rozwiązanie - (optimus z lat. Best) jest najlepszym rozwiązaniem, ale nie może być najlepszego rozwiązania we wszystkich zmysłach. Może być najlepszy tylko w jednym ściśle ustalonym sensie.
Osoba podejmująca decyzje musi dokładnie przedstawić, jaka jest optymalność rozwiązania, tj. według jakich kryteriów (kriterio - miara, ocena) podjęta decyzja musi być optymalna.
Kryterium nazywa się funkcją celu (TF). Korzystając z tego kryterium, można ocenić zarówno pożądane cechy (na przykład zysk, wydajność, niezawodność), jak i niepożądane (koszty, koszty, przestoje itp.). Następnie w pierwszym przypadku starają się zmaksymalizować kryterium, w drugim - zminimalizować.
Problem ma więc optymalne rozwiązanie, jeśli spełnia dwa wymagania:
- istnieje realna możliwość posiadania więcej niż jednego rozwiązania, tj. istnieją ważne rozwiązania;
- istnieje kryterium, które pokazuje, w jakim sensie decyzja powinna być optymalna, tj. najlepsze możliwe.
Zadania optymalizacyjne, których algorytmy mogą być implementowane przy użyciu arkuszy kalkulacyjnych
Różne zadania optymalizacji zawartości można rozwiązać za pomocą MS EXCEL. Rozważ klasyfikację według typów modeli matematycznych, które zawierają następujące elementy:
- surowe dane;
- wymagane zmienne;
- zależności.
Patrz rys. 7.1
Wstępne dane modelu matematycznego to:
- FF - F (xj);
- lewa strona ograniczeń to gi (xj);
- ich prawe boki są bi
Dane bazowe - mogą być deterministyczne lub losowe.
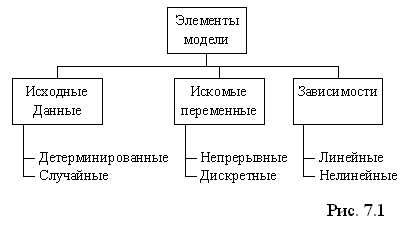
Dane deterministyczne - takie dane źródłowe, gdy podczas przygotowywania modelu ich wartości są znane. Dane losowe - takie dane źródłowe, jeśli ich dokładna wartość nie jest znana z góry.
Wymagane zmienne mogą być ciągłe i dyskretne.
Ciągłe to te wielkości, które w danym GRU mogą przyjmować dowolne wartości. Zmienne dyskretne to takie, które mogą przyjmować tylko podane wartości. Zmienne całkowite to takie zmienne dyskretne, które mogą przyjmować tylko wartości całkowite.
Zależności między zmiennymi (zarówno funkcje obiektywne, jak i ograniczenia) mogą być liniowe i nieliniowe. Liniowe to te zależności, w których zmienne są zawarte w pierwszym stopniu i wykonywane są tylko operacje dodawania i odejmowania. W przeciwnym razie, jeśli zmienne nie są uwzględnione w pierwszym stopniu lub wykonywane są na nich inne operacje (oprócz dodawania i odejmowania), to zależności nazywane są nieliniowymi.
Połączenie różnych elementów modelu tworzy różne klasy problemów optymalizacyjnych:
Surowe dane
Szukane zmienne
Zależności
Klasy zadań
Deterministyczne ciągłe liniowe liniowe programowanie Deterministyczne całkowite Liniowe całkowite programowanie Deterministyczne ciągłe, całkowite Nieliniowe nieliniowe programowanie Losowe ciągłe liniowe stochastyczne programowanie
Główne etapy pracy w rozwiązaniu problemu optymalizacji
- Wybór modelu jest najważniejszym i czasochłonnym zagadnieniem. Jeśli model zostanie wybrany bezskutecznie, to jest to stracony czas i rozczarowanie metodami optymalizacji. Podstawowe wymagania, które musi spełniać model:
- powinny istnieć co najmniej dwie opcje dla wartości parametrów, które spełniają GRU i GRU, ponieważ jeśli nie ma opcji rozwiązania, nie ma nic do wyboru;
- musisz jasno wiedzieć, w jakim sensie pożądane rozwiązanie powinno być najlepsze, w przeciwnym razie ani metody matematyczne, ani komputer nie mogą pomóc.
Wybór modelu kończy się na jego treści.
- Oświadczenie dotyczące treści. Elementy modelu matematycznego powinny być jasno określone:
- surowe dane (deterministyczne i losowe);
- pożądane zmienne (ciągłe i dyskretne);
- granice, w których wartości pożądanych ilości można znaleźć w optymalnym roztworze;
- zależności między zmiennymi (liniowymi lub nieliniowymi);
- kryteria, według których można znaleźć optymalne rozwiązanie.
- Kompilacja modelu matematycznego.
- Gromadzenie podstawowych danych jest niezbędnym etapem w poszukiwaniu optymalnego rozwiązania. Wskazane jest, aby rozpocząć rozwiązywanie problemów o dużym wymiarze za pomocą przykładu testowego. Będzie to wymagało zebrania niewielkiej ilości danych wejściowych na początkowym etapie pracy w celu szybkiej oceny poprawności modelu. Brak dobrej zbieżności algorytmu, prędkości i pamięci operacyjnej komputera nie zastąpi wiarygodności oryginalnych danych (żadne kombajny nie zastąpią jakości nasion).
- Rozwiązanie problemu. Komputer wykorzystujący oprogramowanie aplikacyjne (oprogramowanie) implementuje algorytm znajdowania optymalnego rozwiązania.
- Analiza decyzji jest najważniejszym narzędziem do podejmowania optymalnych decyzji.
- Podjęcie najlepszej decyzji jest ostatnim etapem pracy. Decyzje nie są podejmowane przez komputer, ale przez osobę, która powinna być odpowiedzialna za wyniki podjętej decyzji.
- Graficzne przedstawienie wyniku decyzji i analizy jest ważnym czynnikiem w widoczności informacji niezbędnych do podjęcia decyzji.
do tyłu treść naprzód
