Математичне моделювання
- дає швидку відповідь на поставлене запитання (в реальній обстановці рішення вимагає роки);
- надає можливість широкого експериментування (здійснення на реальному об'єкті часто неможливо).
Правила для успішного математичного моделювання:
- Враховувати основні характеристики об'єкта, що моделюється.
- Нехтувати його другорядними властивостями.
- Вміти виділити основні властивості від другорядних.
Приклад математичної моделі
Завдання. Спроектувати бак, який має форму прямокутного паралелепіпеда, об'ємом V = 2000 м3, так щоб на його виготовлення пішло якомога менше матеріалу.
Рішення.
Обсяг бака можна обчислити за формулою: V = abh, (7.1)
площа S = 2ab + 2ah + 2bh (7.2), де a, b, h- боку бака.
Таку постановку можна записати: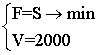 
(7.3),
що читається: мінімізувати величину S за умови, що V = 2000. Підставивши в (7.3) значення V (7.1) і S (7.2), отримаємо: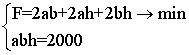 
(7.4),
Додамо очевидне, що a, b, h> 0, отримаємо математичну модель: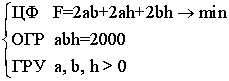 
(7.5),
де: ЦФ - цільова функція, ОГР - обмеження, ГРУ - граничні умови
Загальний випадок задачі оптимізації
Позначимо х1 = а, x2 = b, x3 = h, тоді запишемо: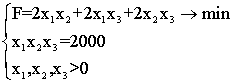 
(7.6),
Очевидно, що (7.6) можна записати: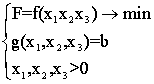 
(7.7),
Тоді в загальному випадку можна записати так: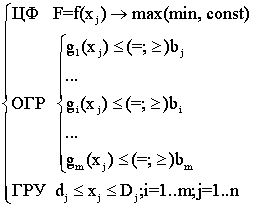 
(7.8),
Систему (7.8) прийнято записувати більш компактно:
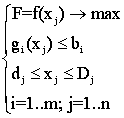(7.9)
Запис (7.9) є загальною формою записи завдань оптимізації. У цю систему входять три складові:
- ЦФ - цільова функція або критерій оптимізації, показує, в якому сенсі рішення повинно бути оптимальним, тобто найкращим. При цьому можливі 3 види призначення цільової функції:
- Максимізація.
- Мінімізація.
- Призначення заданого значення.
- ОГР - обмеження, встановлюють залежності між змінними. Вони можуть бути односторонніми: gi (xj) ≤bi, або двосторонніми: ai≤gi (xj) ≤bi. Причому будь-який двосторонньо обмеження можна записати в вигляді двох односторонніх: gi (xj) ≥ai, gi (xj) ≤bi.
- ГРУ - граничні умови. Показують, в яких межах можуть бути значення шуканих змінних в оптимальному рішенні.
Рішення завдання, що задовольняють всім обмеженням і граничним умовам, називаються припустимими. Якщо математична модель складена правильно, то ми будемо мати цілий ряд допустимих рішень.
Важливою характеристикою завдання оптимізації є її розмірність, яка визначається числом змінних n і числом обмежень m. Співвідношення цих величин є визначальним при постановці завдання оптимізації. Можливі три співвідношення n <m, n = m, n> m.
- n <m
наприклад: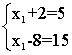
Тут n = 1, m = 2. Очевидно, що такі завдання рішення не мають, за винятком випадку лінійно залежною системи рівнянь: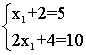
(То ж що випадок 2, при n = m = 1) - n = m
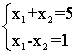
Тут n = m = 2. Існує єдине рішення, за винятком випадку лінійно залежною системи рівнянь: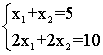
(Те саме, що випадок 3, при n = 2, m = 1) - n> m
x1 + x2 = 5
Тут n = 2, m = 1. Існує безліч рішень.
Так як більшість обмежень записуються у вигляді нерівностей, то розглянемо, наприклад, наступна нерівність: х1≤5. Введемо додаткову змінну y1≥0 і перейдемо від заданої нерівності до рівняння: x1 + y1 = 5 Для цього рівняння n = 2, m = 1, і отже воно має безліч рішень.
У загальному випадку ОГР мають вигляд: gi (xj) ≤bi i = 1..m; j = 1..n;
то їх можна записати в вигляді: gi (xj) + yi = bi yi≥0; i = 1..m; j = 1..n.
У цьому випадку загальна кількість змінних xj і yi, рівне N буде: N = n + m, а число рівнянь залишиться колишнім рівним m.
Очевидно, що N = n + m> m, і система має незліченну безліч рішень. Значить, якщо обмеженнями є нерівності, то система завжди має безліч рішень.
Т.ч. умова n> m - це неодмінна вимога завдань оптимізації.
Оптимальне рішення - (optimus від лат. Найкращий) це найкраще рішення, але найкращого рішення у всіх сенсах бути не може. Може бути кращим тільки в одному, строго встановленому сенсі.
Приймає рішення повинен абсолютно точно представляти, в чому полягає оптимальність рішення, тобто за яким критерієм (kriterio - мірило, оцінка) прийняте рішення має бути оптимальним.
Критерій називають цільовою функцією (ЦФ). За допомогою критерію можна оцінювати якості як бажані (наприклад прибуток, продуктивність, надійність), так і небажані (витрати, витрати, простої і т.д.). Тоді в першому випадку прагнуть до максимізації критерію, у другому - до мінімізації.
Отже, завдання має оптимальне рішення, якщо вона задовольняє двом вимогам:
- є реальна можливість мати більше одного рішення, тобто існують допустимі рішення;
- є критерій, що показує, в якому сенсі прийняте рішення має бути оптимальним, тобто найкращим з допустимих.
Завдання оптимізації, алгоритми яких можуть бути реалізовані за допомогою електронних таблиць
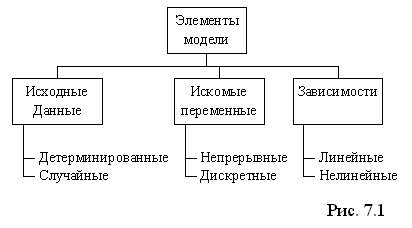
Різні за змістом задачі оптимізації можна вирішувати за допомогою MS EXCEL. Розглянемо класифікацію по виду математичних моделей, які включають в себе наступні елементи:
- вихідні дані;
- шукані змінні;
- залежності.
Див. Мал. 7.1
Вихідними даними для математичної моделі є:
- ЦФ - F (xj);
- ліві частини обмежень - gi (xj);
- їх праві частини - bi
Вихідні дані - можуть бути детермінованими або випадковими.
Детерміновані дані - такі вихідні дані, коли при складанні моделі їх значення відомі. Випадкові дані - такі вихідні дані, якщо точне їх значення заздалегідь невідомо.
Шукані змінні - можуть бути безперервними і дискретними.
Безперервними називаються такі величини, які в заданих ГРУ можуть приймати будь-які значення. Дискретними називаються такі змінні, які можуть приймати тільки задані значення. Цілочисельними називаються такі дискретні змінні, які можуть приймати тільки цілі значення.
Залежності між змінними (як цільові функції, так і обмеження) можуть бути лінійними і нелінійними. Лінійними називаються такі залежності, в які змінні входять в першого ступеня і з ними виконуються тільки дії додавання і віднімання. Інакше, якщо змінні входять не в першого ступеня або над ними виконуються інші (крім додавання і віднімання) операції, то залежно називаються нелінійними.
Поєднання різних елементів моделі утворюють різні класи задач оптимізації:
Вихідні дані
шукані змінні
залежності
класи задач
Детерміновані Безперервні Лінійні Лінійного програмування детерміновані Цілочисельні Лінійні цілочисельного програмування детерміновані Безперервні, цілочисельні Нелінійні Нелінійного програмування Випадкові Безперервні Лінійні стохастичного програмування
Основні етапи робіт при вирішенні задачі оптимізації
- Вибір моделі - найважливіше питання, що вимагає багато часу. Якщо модель обрана невдало, то це втрачений час і розчарування в методах оптимізації. Основні вимоги, яким повинна задовольняти модель:
- має існувати, як мінімум, два варіанти значень параметрів, що задовольняють ОГР і ГРУ, адже якщо варіантів рішення немає, значить, і вибирати нема з чого;
- треба чітко знати, в якому сенсі шукане рішення має бути найкращим, інакше не допоможуть ні математичні методи, ні ПК.
Вибір моделі завершується її змістовної постановкою.
- Змістовна постановка. Повинні бути чітко сформульовані елементи математичної моделі:
- вихідні дані (детерміновані і випадкові);
- шукані змінні (безперервні і дискретні);
- межі, в яких можуть знаходитися значення шуканих величин в оптимальному рішенні;
- залежності між змінними (лінійні або нелінійні);
- критерії, за якими слід знаходити оптимальне рішення.
- Складання математичної моделі.
- Збір вихідних даних - необхідний етап роботи при пошуку оптимального рішення. Рішення задач великої розмірності доцільно почати з контрольного прикладу. Це зажадає зібрати на початковому етапі роботи невелика кількість вихідних даних для швидкої оцінки правильності складеної моделі. Ніяка хороша збіжність алгоритму, швидкодія і оперативна пам'ять ПК не замінять достовірності вихідних даних (ніякі комбайни не замінять якісного насіння).
- Рішення задачі. Комп'ютер за допомогою прикладних програм (програмного забезпечення) реалізує алгоритм пошуку оптимального рішення.
- Аналіз рішення - найважливіший інструмент прийняття оптимальних рішень.
- Ухвалення оптимального рішення - кінцевий етап роботи. Рішення приймає не комп'ютер, а людина, яка мусить відповідати за результати прийнятого рішення.
- Графічне представлення результату рішення і аналізу - потужний фактор наочності інформації, необхідної для прийняття рішення.
назад зміст вперед
