матэматычнае мадэляванне
- дае хуткі адказ на пастаўленае пытанне (у рэальнай абстаноўцы рашэнне патрабуе гады);
- прадастаўляе магчымасць шырокага эксперыментавання (ажыццяўленне на рэальным аб'екце часта немагчыма).
Правілы для паспяховага матэматычнага мадэлявання:
- Ўлічваць галоўныя ўласцівасці мадэляваных аб'екта.
- Грэбаваць яго другараднымі ўласцівасцямі.
- Умець аддзяліць галоўныя ўласцівасці ад другарадных.
Прыклад матэматычнай мадэлі
Задача. Спраектаваць бак, які мае форму прастакутнага паралелепіпеда, аб'ёмам V = 2000 м3, так каб на яго выраб пайшло як мага менш матэрыялу.
Рашэнне.
Аб'ём бака можна вылічыць па формуле: V = abh, (7.1)
плошчу S = 2ab + 2ah + 2bh (7.2), дзе a, b, h- боку бака.
Такую пастаноўку можна запісаць: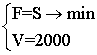 
(7.3),
што чытаецца: мінімізаваць велічыню S пры ўмове, што V = 2000. Падставіўшы ў (7.3) значэнні V (7.1) і S (7.2), атрымаем: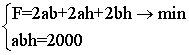 
(7.4),
Дадамо відавочнае, што a, b, h> 0, атрымаем матэматычную мадэль: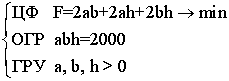 
(7.5),
дзе: ЦФ - мэтавая функцыя, ОГР - абмежаванні, ГРУ - межавыя ўмовы
Агульны выпадак задачы аптымізацыі
Абазначым х1 = а, x2 = b, x3 = h, тады запішам: 
(7.6),
Відавочна, што (7.6) можна запісаць: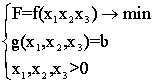 
(7.7),
Тады ў агульным выпадку можна запісаць так: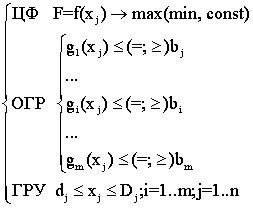 
(7.8),
Сістэму (7.8) прынята запісваць больш кампактна:
(7.9)
Запіс (7.9) з'яўляецца агульнай формай запісу задач аптымізацыі. У гэтую сістэму ўваходзяць тры складнікі:
- ЦФ - мэтавая функцыя або крытэр аптымізацыі, паказвае, у якім сэнсе рашэнне павінна быць аптымальным, г.зн. найлепшым. Пры гэтым магчымыя 3 выгляду прызначэння мэтавай функцыі:
- Максімізацыя.
- Мінімізацыя.
- Прызначэнне зададзенага значэння.
- ОГР - абмежаванне, усталёўваюць залежнасці паміж зменнымі. Яны могуць быць аднабаковымі: gi (xj) ≤bi, або двухбаковымі: ai≤gi (xj) ≤bi. Прычым любое двухбакова абмежаванне можна запісаць у выглядзе двух аднабаковых: gi (xj) ≥ai, gi (xj) ≤bi.
- ГРУ - межавыя ўмовы. Паказваюць, у якіх межах могуць быць значэнні шуканых зменных ў аптымальным рашэнні.
Рашэння задачы, якія задавальняюць усім абмежаванням і межавым умовам, называюцца дапушчальнымі. Калі матэматычная мадэль складзена правільна, то мы будзем мець цэлы шэраг дапушчальных рашэнняў.
Важнай характарыстыкай задачы аптымізацыі з'яўляецца яе памернасць, вызначаная лікам зменных n і лікам абмежаванняў m. Суадносіны гэтых велічынь з'яўляецца вызначальным пры пастаноўцы задачы аптымізацыі. Магчымыя тры суадносін n <m, n = m, n> m.
- n <m
напрыклад: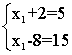
Тут n = 1, m = 2. Відавочна, што такія задачы рашэнні не маюць, за выключэннем выпадку лінейна залежнай сістэмы раўнанняў: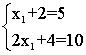
(Тое ж што выпадак 2, пры n = m = 1) - n = m
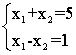
Тут n = m = 2. Існуе адзінае рашэнне, за выключэннем выпадку лінейна залежнай сістэмы раўнанняў: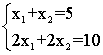
(Тое ж, што выпадак 3, пры n = 2, m = 1) - n> m
x1 + x2 = 5
Тут n = 2, m = 1. Існуе бясконцае мноства рашэнняў.
Так як большасць абмежаванняў запісваюцца ў выглядзе няроўнасцей, то разгледзім, напрыклад, наступнае няроўнасць: х1≤5. Ўвядзем дадатковую зменную y1≥0 і пяройдзем ад зададзенага няроўнасці да раўнанні: x1 + y1 = 5 Для гэтага раўнання n = 2, m = 1, і такім чынам яно мае бясконцае мноства рашэнняў.
У агульным выпадку ОГР маюць выгляд: gi (xj) ≤bi i = 1..m; j = 1..n;
то іх можна запісаць у выглядзе: gi (xj) + yi = bi yi≥0; i = 1..m; j = 1..n.
У гэтым выпадку агульная колькасць зменных xj і yi, роўнае N будзе: N = n + m, а лік раўнанняў застанецца ранейшым роўным m.
Відавочна, што N = n + m> m, і сістэма мае незлічонае мноства рашэнняў. Значыць, калі абмежаваннямі з'яўляюцца няроўнасці, то сістэма заўсёды мае незлічонае мноства рашэнняў.
Т.ч. ўмова n> m - гэта абавязковае патрабаванне задач аптымізацыі.
Аптымальнае рашэнне - (optimus ад лац. Найлепшы) гэта найлепшае рашэнне, але найлепшага рашэнні ва ўсіх сэнсах быць не можа. Можа быць лепшым толькі ў адным, строга вызначаным сэнсе.
Які прымае рашэнне павінен абсалютна дакладна ўяўляць, у чым заключаецца аптымальнасць рашэння, г.зн. па якім крытэры (kriterio - мерка, ацэнка) якое прымаецца рашэнне павінна быць аптымальным.
Крытэрый называюць мэтавай функцыяй (ЦФ). З дапамогай крытэра можна ацэньваць якасці як пажаданыя (напрыклад прыбытак, прадукцыйнасць, надзейнасць), так і непажаданыя (выдаткі, выдаткі, прастоі і г.д.). Тады ў першым выпадку імкнуцца да максімізацыі крытэра, у другім - да мінімізацыі.
Такім чынам, задача мае аптымальнае рашэнне, калі яна задавальняе двум патрабаванням:
- ёсць рэальная магчымасць мець больш аднаго рашэння, г.зн. існуюць дапушчальныя рашэння;
- маецца крытэрый, які паказвае, у якім сэнсе якое прымаецца рашэнне павінна быць аптымальным, г.зн. найлепшым з дапушчальных.
Задачы аптымізацыі, алгарытмы якіх могуць быць рэалізаваны з дапамогай электронных табліц
Розныя па змесце задачы аптымізацыі можна вырашаць з дапамогай MS EXCEL. Разгледзім класіфікацыю па выглядзе матэматычных мадэляў, якія ўключаюць у сябе наступныя элементы:
- зыходныя дадзеныя;
- шуканыя зменныя;
- залежнасці.
Гл. Мал. 7.1
Зыходнымі дадзенымі для матэматычнай мадэлі з'яўляюцца:
- ЦФ - F (xj);
- левыя часткі абмежаванняў - gi (xj);
- іх правыя часткі - bi
Зыходныя дадзеныя - могуць быць дэтэрмінаванымі або выпадковымі.
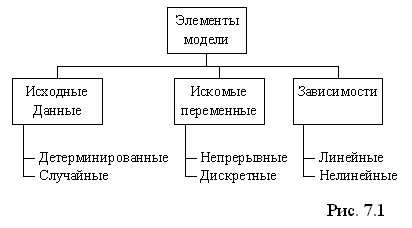
Дэтэрмінаваных дадзеныя - такія зыходныя дадзеныя, калі пры складанні мадэлі іх значэння вядомыя. Выпадковыя дадзеныя - такія зыходныя дадзеныя, калі дакладнае іх значэнне загадзя невядома.
Шуканыя зменныя - могуць быць бесперапыннымі і дыскрэтнымі.
Бесперапыннымі называюцца такія велічыні, якія ў зададзеных ГРУ могуць прымаць любыя значэння. Дыскрэтнымі называюцца такія зменныя, якія могуць прымаць толькі зададзеныя значэнні. Цэлалікавымі называюцца такія дыскрэтныя зменныя, якія могуць прымаць толькі цэлыя значэння.
Залежнасці паміж зменнымі (як мэтавыя функцыі, так і абмежаванні) могуць быць лінейнымі і нелінейнымі. Лінейнымі называюцца такія залежнасці, у якія зменныя ўваходзяць у першай ступені і з імі выконваюцца толькі дзеянні складання і аднімання. Інакш, калі зменныя ўваходзяць не ў першай ступені або над імі выконваюцца іншыя (акрамя складання і аднімання) аперацыі, то залежнасці называюцца нелінейнымі.
Спалучэнне розных элементаў мадэлі ўтвараюць розныя класы задач аптымізацыі:
Зыходныя дадзеныя
шуканыя зменныя
залежнасці
класы задач
Дэтэрмінаваных Бесперапынныя Лінейныя лінейна праграмавання дэтэрмінаваных цэлалікавых Лінейныя цэлалікавых праграмавання дэтэрмінаваных Бесперапынныя, цэлалікавых Нелінейныя нелінейнага праграмавання Выпадковыя Бесперапынныя Лінейныя стахастычнага праграмавання
Асноўныя этапы работ пры рашэнні задачы аптымізацыі
- Выбар мадэлі - найважнейшы пытанне, які патрабуе шмат часу. Калі мадэль абраная няўдала, то гэта страчаны час і расчараванне ў метадах аптымізацыі. Асноўныя патрабаванні, якім павінна задавальняць мадэль:
- павінна існаваць, як мінімум, два варыянты значэнняў параметраў, якія задавальняюць ОГР і ГРУ, бо калі варыянтаў рашэння няма, значыць, і выбіраць няма з чаго;
- трэба дакладна ведаць, у якім сэнсе шуканае рашэнне павінна быць найлепшым, інакш не дапамогуць ні матэматычныя метады, ні ПК.
Выбар мадэлі завяршаецца яе змястоўнай пастаноўкай.
- Змястоўная пастаноўка. Павінны быць дакладна сфармуляваны элементы матэматычнай мадэлі:
- зыходныя дадзеныя (дэтэрмінаваных і выпадковыя);
- шуканыя зменныя (бесперапынныя і дыскрэтныя);
- межы, у якіх могуць знаходзіцца значэння шуканых велічынь у аптымальным рашэнні;
- залежнасці паміж зменнымі (лінейныя або нелінейныя);
- крытэрыі, па якіх варта знаходзіць аптымальнае рашэнне.
- Складанне матэматычнай мадэлі.
- Збор зыходных дадзеных - неабходны этап працы пры пошуку аптымальнага рашэння. Рашэнне задач вялікай памернасці мэтазгодна пачаць з кантрольнага прыкладу. Гэта запатрабуе сабраць на пачатковым этапе працы невялікая колькасць зыходных дадзеных для хуткай ацэнкі правільнасці складзенай мадэлі. Ніякая добрая збежнасць алгарытму, хуткадзейнасць і аператыўная памяць ПК не заменяць дакладнасці зыходных дадзеных (ніякія камбайны не заменяць якаснага насення).
- Рашэнне задачы. Кампутар з дапамогай прыкладных праграм (праграмнага забеспячэння) рэалізуе алгарытм пошуку аптымальнага рашэння.
- Аналіз рашэння - найважнейшы інструмент прыняцця аптымальных рашэнняў.
- Прыняцце аптымальнага рашэння - канчатковы этап работы. Рашэнні прымае не кампутар, а чалавек, які і павінен адказваць за вынікі прынятага рашэння.
- Графічнае прадстаўленне выніку рашэння і аналізу - магутны фактар нагляднасці інфармацыі, неабходнай для прыняцця рашэння.
назад змест наперад
